วงโคจรรูปวงรี

วงโคจรรูปวงรี
Credit: Horvath and Rubber Duckรูปวงรีเป็นเสมือนรูปวงกลมที่ถูกบีบให้เรียวขึ้นจนมีจุดโฟกัสอยู่ 2 จุด ดาวเคราะห์จะโคจรไปรอบดวงอาทิตย์บนวงโคจรรูปวงรี บนแผนภาพทางขวานี้จะเห็นว่าดวงอาทิตย์อยู่บนจุดโฟกัสเพียงจุดหนึ่ง ส่วนอีกจุดโฟกัสหนึ่งจะไม่มีอะไรอยู่ตรงนั้น (จุดสีดำในแผนภาพ) และดาวเคราะห์จะโคจรไปตามวงโคจรรูปวงรี

วงโคจรจะมีความเรียวหรือ “ความแบน” มากน้อยแค่ไหน ดูได้ผ่านค่าที่เรียกว่า “ความเยื้องศูนย์กลาง” (Eccentricity) ยิ่งวงโคจรเรียวมากเท่าไหร่ ค่าความเยื้องศูนย์กลางของวงโคจรจะมีค่ามากขึ้นตามไป รูปวงกลมมีค่าความเยื้องศูนย์กลางเป็น 0 เมื่อวงกลมถูกบีบให้เรียวแบนขึ้นจะกลายเป็นวงรี วงรีที่เรียวแบนมากๆ จะมีค่าความเยื้องศูนย์กลางเข้าใกล้ 1 ดังนั้น วงรีจะมีค่าความเยื้องศูนย์กลางระหว่าง 0 ถึง 1

วงโคจรของดาวเคราะห์ทุกดวงเป็นรูปวงรี แต่วงโคจรเหล่านี้ส่วนใหญ่จะมีค่าความเยื้องศูนย์กลางน้อยจะดูเกือบเป็นวงกลม แต่ในกรณีวงโคจรของดาวพุธ (รวมถึงวงโคจรของดาวพลูโต ถึงแม้ดาวดวงนี้จะไม่ใช่ดาวเคราะห์แล้วก็ตาม) จะมีค่าความเยื้องศูนย์กลางมากจนดูเป็นวงรีชัดเจนขึ้น

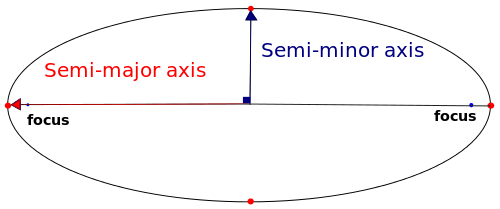
แกนต่างๆของวงรี
Credit: Sae1962แกนยาว (ด้านยาว) ของวงรีเรียกว่า “แกนเอก” ขณะที่แกนสั้น (ด้านกว้าง) ของวงรีเรียกว่า “แกนโท” ครึ่งหนึ่งของแกนเอกจะเรียกว่า “กึ่งแกนเอก” และครึ่งหนึ่งของแกนโทจะเรียกว่า “กึ่งแกนโท”

เรื่องวงโคจรรูปวงรีและ “กึ่งแกนเอก” ของวงโคจรเกี่ยวข้องกับกฏ 3 ข้อที่ใช้อธิบายการเคลื่อนที่ของดาวเคราะห์รอบดาวฤกษ์ เรียกว่า “กฏการโคจรของเคปเลอร์” ซึ่งได้อธิบายไว้ในวีดีโอขององค์การอวกาศยุโรป (ESA) คลิปนี้